Ecuación de segundo grado a partir de sus soluciones y suma y producto de raíces

Construcción de una ecuación de segundo grado a partir de sus soluciones

Vamos a ver ahora la manera en cómo se puede construir una ecuación de segundo grado cuando se conocen las soluciones.

Ejemplo

Las soluciones de la ecuación $x^{2} + 2 x - 3 = 0$ son:

$x = \frac{- 2 \pm \sqrt{4 + 12}}{2} = \frac{- 2 \pm 4}{2} = {\begin{matrix} x_{1} = 1 \\ x_{2} = - 3 \end{matrix}$

Observemos ahora qué sucede cuando hacemos el producto $(x - x_{1}) \cdot (x - x_{2})$

$(x - 1) \cdot (x + 3) = x^{2} - x + 3 x - 3 = x^{2} + 2 x - 3$ Hemos llegado pues a la ecuación original.

De manera que "el producto de equis menos una raíz por equis menos la otra raíz es igual a la ecuación de segundo grado que tiene como soluciones dichas raíces".

Ejemplo

Si las soluciones de la ecuación son $x_{1} = 4, x_{2} = 2$ la ecuación correspondiente de segundo grado es:

$(x - 4) (x - 2) = x^{2} - 6 x + 8 = 0$

Ejemplo

Si las raíces de la ecuación son $x_{1} = - 2, x_{2} = - 5$ la ecuación correspondiente de segundo grado es:

$(x + 1) (x + 5) = x^{2} + 6 x + 5 = 0$

Ejemplo

Si las soluciones de la ecuación son $x_{1} = 3, x_{2} = - \frac{2}{3}$ la ecuación correspondiente de segundo grado es:

$(x - 3) (x + \frac{2}{3}) = x^{2} - \frac{7}{3} x - 2 = 0$

Ejemplo

Si las raíces de la ecuación son $x_{1} = 0, x_{2} = 16$ la ecuación correspondiente de segundo grado es:

$(x - 0) (x - 16) = x^{2} + 16 x = 0$

Reconstrucción de una ecuación de segundo grado a partir de la suma y el producto de raíces

Sabemos que $(x - x_{1}) \cdot (x - x_{2})$ conduce a la ecuación que tiene a $x_{1}, x_{2}$ como soluciones. Si efectuamos este producto:

$(x - x_{1}) \cdot (x - x_{2}) = x^{2} - x_{1} x - x_{2} x + x_{1} x_{2} = x^{2} - (x_{1} + x_{2}) x + x_{1} x_{2}$

expresión en la que aparecen la suma y el producto de raíces a los que podemos llamar $s$ y $p$ .

$s = x_{1} + x_{2} p = x_{1} \cdot x_{2}$

Con lo que la ecuación de segundo grado adquiere la forma:

$x^{2} - s x + p = 0$

Ejemplo

Construir una ecuación de segundo grado sabiendo que la suma de sus raíces vale $5$ y el producto $6$ .

Tendremos $s = 5, p = 6$ con lo que la ecuación será:

$x^{2} - 5 x + 6 = 0$

Este método es más rápido que el de hacer el producto de raíces.

Veamos otros ejemplos:

Ejemplo

La ecuación de segundo grado que tiene por soluciones $4$ y $9$ es:

$x^{2} - 13 x + 36 = 0$

Ejemplo

La ecuación de segundo grado que tiene por soluciones $- 3$ y $- 5$ es:

$x^{2} + 8 x + 15 = 0$

En principio no es sencillo crear un enunciado que nos conduzca a una ecuación de segundo grado. La manera más sencilla sería escribir literalmente lo que dice la ecuación.

Ejemplo

Si queremos que la solución del problema sea la ecuación $x^{2} - 5 x + 6 = 0$ podemos plantear un enunciado del tipo: Si elevamos una cantidad al cuadrado y luego le restamos cinco veces esa misma cantidad el resultado es menos $6$ ¿Cual es dicha cantidad?

Está claro que es un enunciado más interesante el que dice "Hallar dos números sabiendo que su suma vale $5$ y el producto $6$ " enunciado que conduce a la misma ecuación y cuyas soluciones son las resultantes de resolver la ecuación propuesta:

$x = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2} = {\begin{matrix} x_{1} = 3 \\ x_{2} = 2 \end{matrix}$

Estos mismos datos nos permiten hacer un planteamiento de tipo geométrico.

Ejemplo

Sabemos que el perímetro de un rectángulo es $10$ y su área $6$ . Calcular los lados de dicho rectángulo.

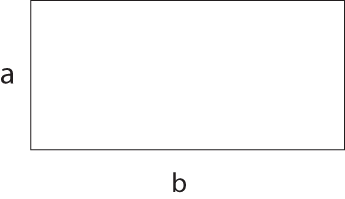
imagen

El perímetro del rectángulo es la suma de todos sus lados, de manera que $a + a + b + b = 2 a + 2 b = 2 (a + b) = 10$ , que es, $a + b = 5$

Por otro lado el área del rectángulo es $a \cdot b = 6$ .

Luego lo que se nos pide es que resolvamos una ecuación de segundo grado en la que la suma de raíces vales $5$ y el producto $6$ , lo que nos lleva a la ecuación $x^{2} - 5 x + 6 = 0$ .

Y la solución es:

$x = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2}$

Con lo que los lados del rectángulo serán $a = 2$ y $b = 3$